果然Deadline是第一生产力。
继新年一周懒懒散散,再加上躺了两三天,眼瞅着寒假快要结束了,然后发现认真下来就能进度很快。
补码一位乘法
原码一位乘法我还能理解它的算法意义,而补码一位乘法就是真的毫无头绪了,也问了问老师,找了找资料,还是一筹莫展,最后只能是照着算法画了出来,也通过了测试。
原理是Booth算法,百科上也给了证明,但只能说头大吧。
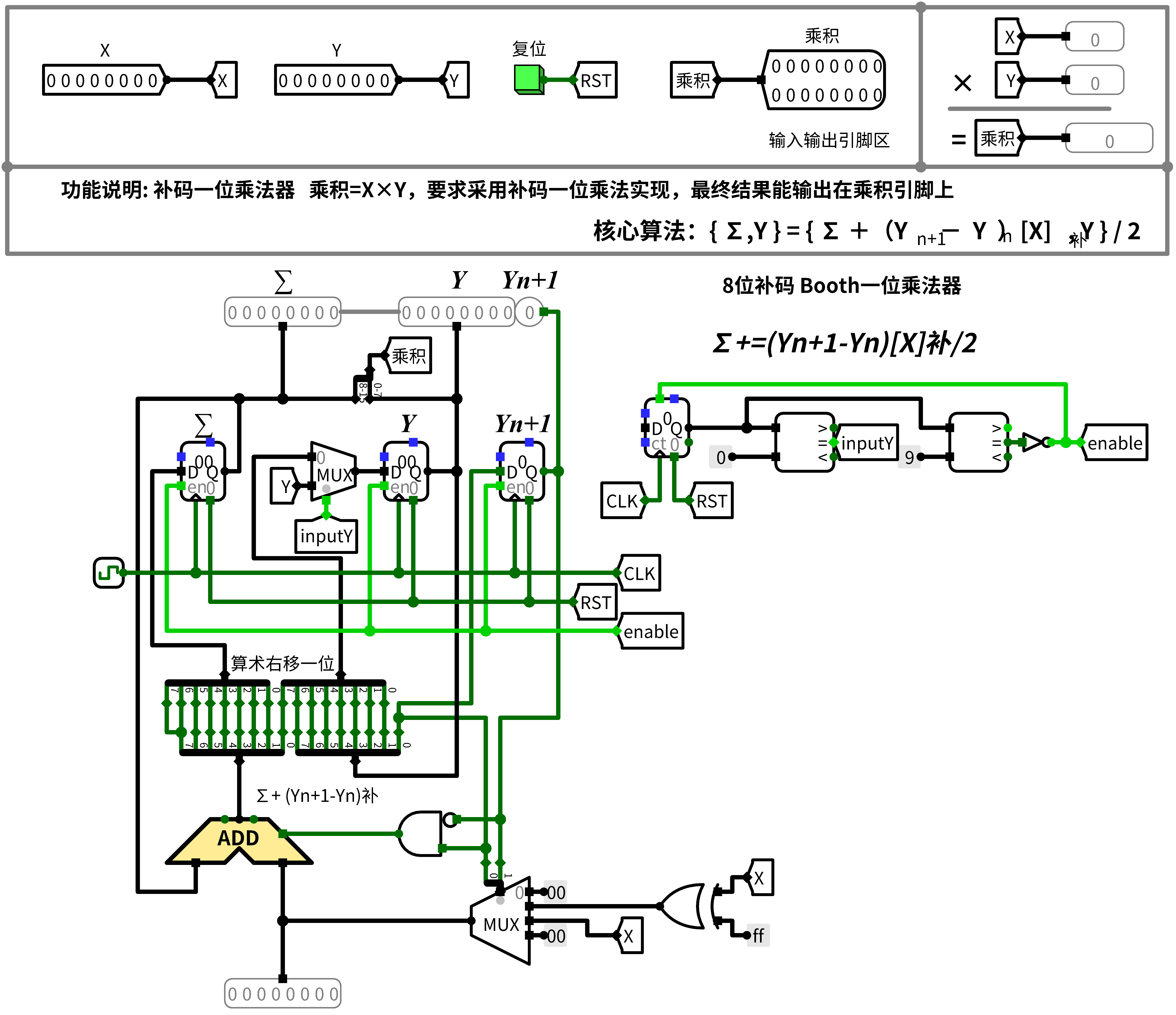
ALU
说是ALU,但其实是一个相当简易的ALU,把各种功能都摆出来,然后接在一起,最后选择一个输出,只能说离真正的ALU还差很多吧,比较简单,没什么好说的。
存储器扩展
接下来的实验是字库电路实验,不过本质上是一个存储器扩展的设计,考试最喜欢出这种题了。
存下所有的汉字字形码需要\(256bit\times16k\)的存储器,然后给了\(7\)个\(32bit\times16k\)的RAM和\(4\)个\(32bit\times4k\)的RAM。
思路自然就是将\(4\)个\(32bit\times4k\)的RAM字扩展为一个\(32bit\times16k\)的整体,使用地址最高两位充当片选信号,这样数据好拆分,然后和剩下的\(7\)个\(32bit\times16k\)的RAM位扩展为\(256bit\times16k\)的存储器。最后把提供的数据加载到各RAM中,然后就会发现有相当多的空余没有数据来着。
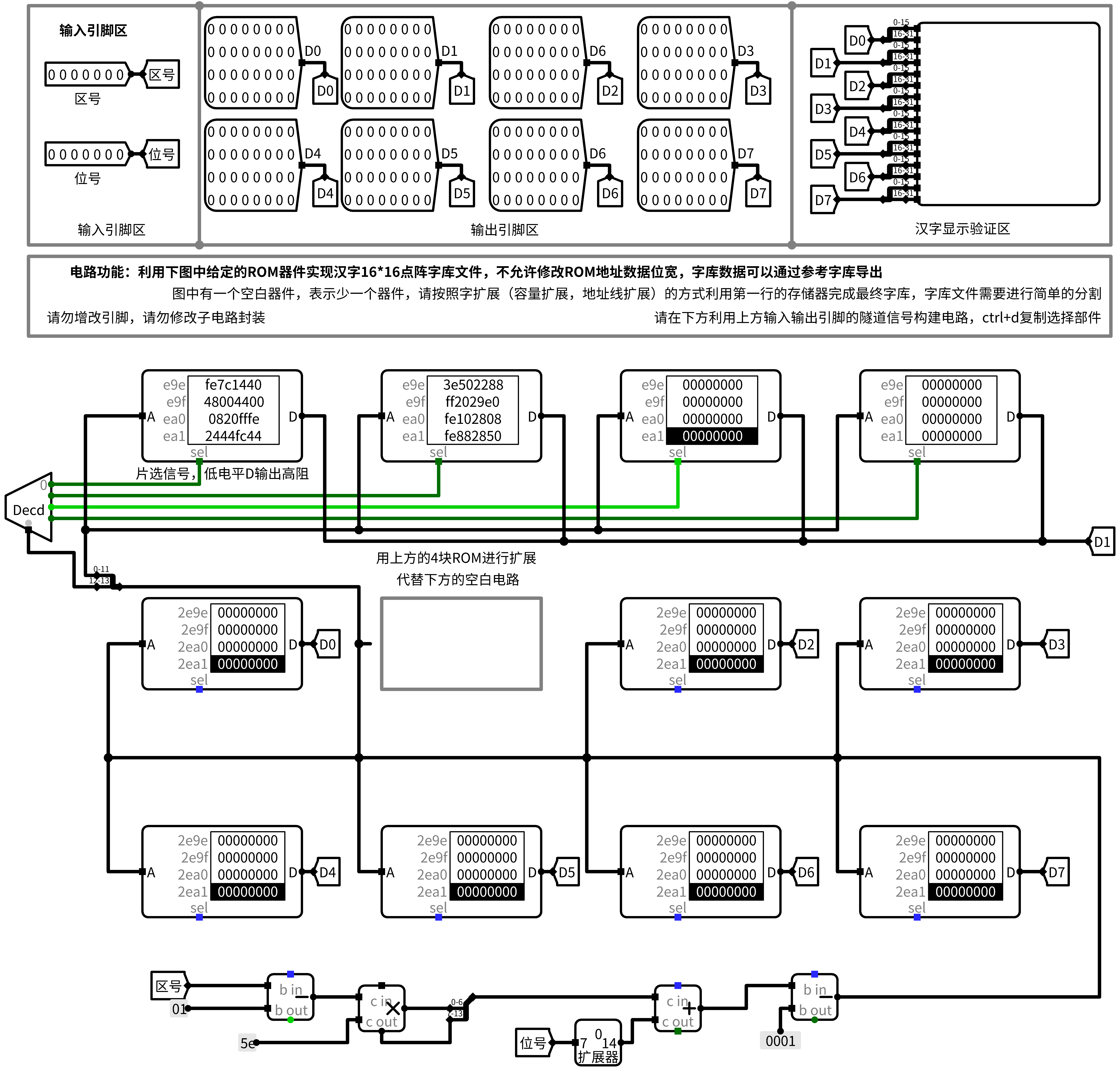
MIPS RAM
这个实验让我第一次了解到了三态门的作用——可以复用数据通路。
实验的目的是可以通过字节,半字,字来存取数据,存取数据时有效数据都放在了最低位,有一点是必须遵守对齐的地址进行存取,否则会强制对齐。
采用了\(4\)个\(8bit\times1k\)的RAM字扩展,不过选取低\(2\)位为片选信号,这样的原因是可以在一个周期内取出连续地址的数据,如果采取高\(2\)位的话,就不能在一个周期内完成,考虑到空间局部性的话,效率就得大打折扣了。
那么如何根据不同的模式将数据送到正确的位置呢?有两种解决思路,多路选择器或者三态门了。
那就对写入和读出采取两种思路来完成电路,输入采用多路选择器,而输出采用三态门。
对于输入,总共可能有七种情形:

观察这\(7\)种情况,可以发现:只有最低字节数据会写入第\(0\)个RAM;最低字节和次低字节数据可能写入第\(1\)个RAM;最低字节和次高字节数据可能写入第\(2\)个RAM;最低字节,次低字节和最高字节都可能写入第\(3\)个RAM。那么,每一个RAM的数据可能来源都已经确定了,通过多路选择器配合mode与访存地址来进行选择。
有一点,为了实现强制对齐,当处于“字写入”模式时,所有的RAM都选择;当处于“半字写入时”,且地址低\(2\)为\(00\)或者\(01\),那么第\(0\)和第\(1\)个RAM都应被选择;当处于“半字写入时”,且地址低\(2\)为\(10\)或者\(11\),那么第\(2\)和第\(3\)个RAM都应被选择;当处于“字节写入”模式时,就只选择对应的一个RAM。
综上,画出来的输入电路是这样的:
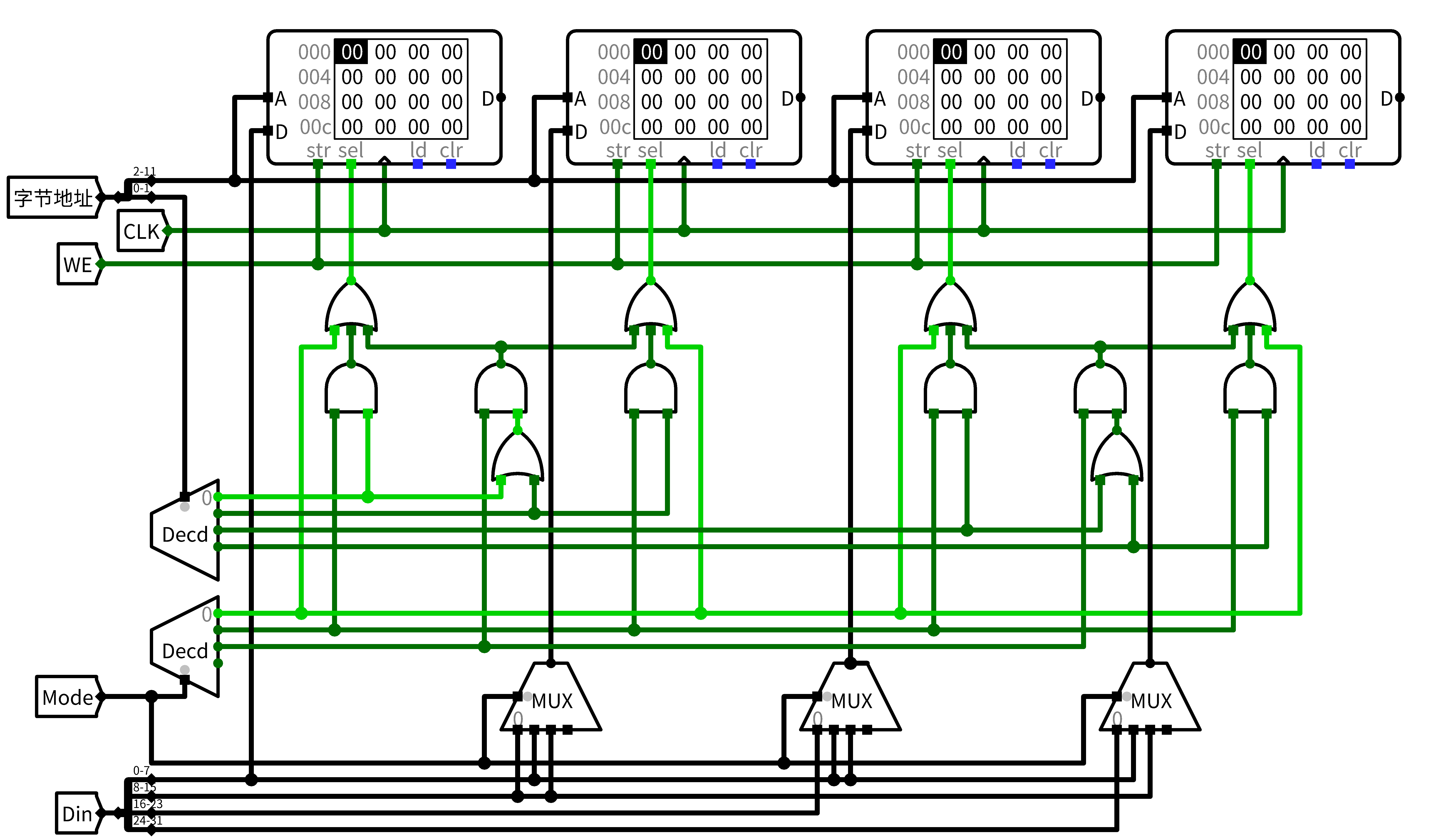
然后是三态门控制的读出。
三态门可以看做是一扇建立在电路中的门,打开后电信号可以通过,而一旦关闭,电信号无法通过,形成高阻态,相当于断路。借助这个性质,就可以把所有可能的通路连接在一起,通过三态门精确控制数据的源头与目标。
读出的情形和写入类似:

读出的方式可以通过mode确定,高低位可以使用地址的低\(2\)位确定,那么就可以得出\(7\)条类似“高半字节读出时,第\(3\)个RAM读出到次低字节,第\(2\)个RAM读出到最低字节”这样的结论,通过这\(7\)条结论可以得出\(8\)个类似“第\(0\),\(1\),\(2\),\(3\)个RAM通向最低位”这样的通路,每条通路上放上一个三态门,通过mode控制哪些通路打开,哪些关闭,读出就这么完成了。
配合上相同的强制对齐,再把高阻态拉到\(0\),读出的电路也出来了:
合二为一:
MIPS Regfile
这个实验也简单,就是译码器和多路选择器的灵活使用,简单到甚至能出到卷子上当考题:
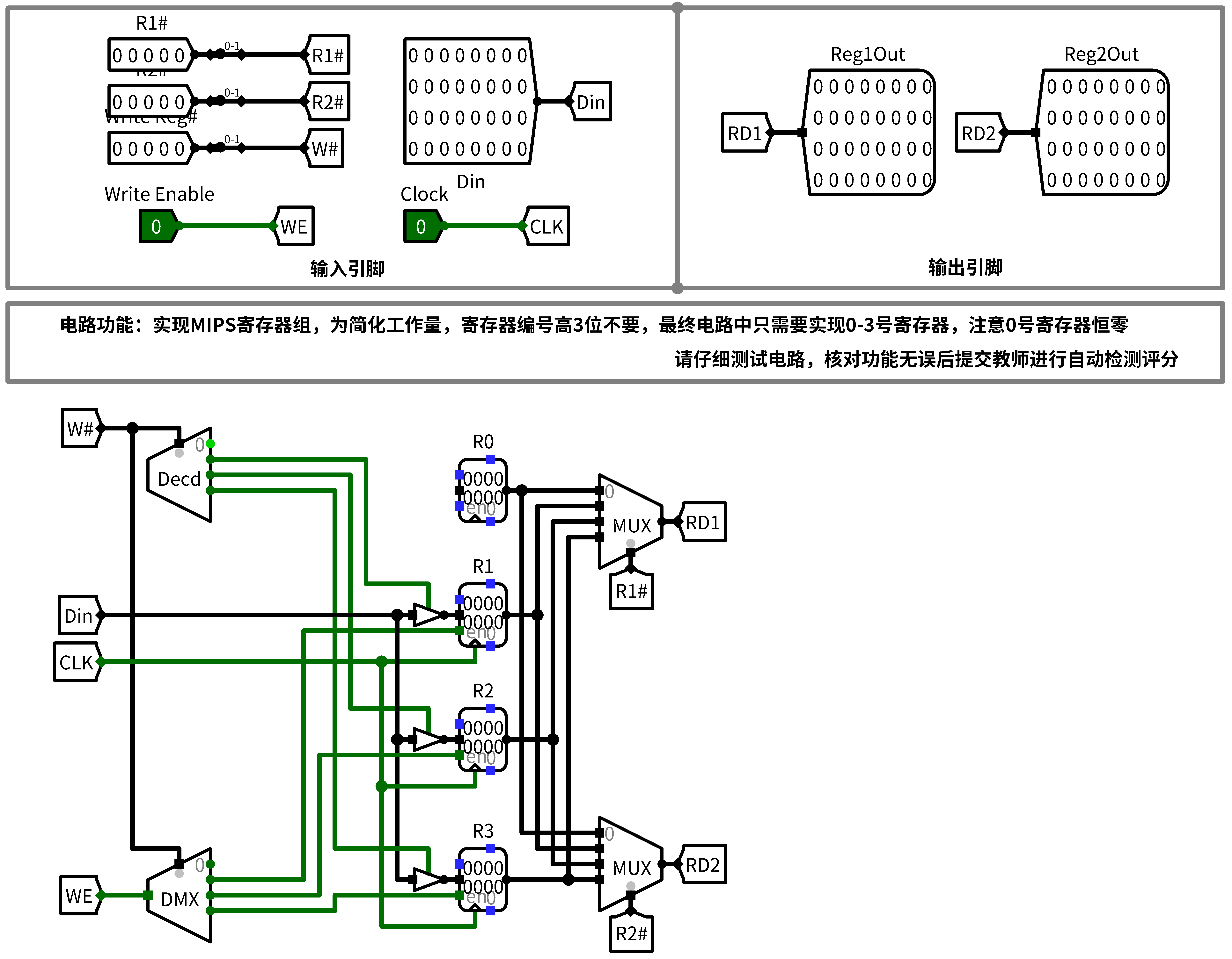
Cache
Cache,又一个必考点,记忆得滚瓜烂熟的那种。Cache的组织方式,替换算法,写回策略,占用计算都相当的灵活,然后根据实验,需要先后完成全相联、直接相联与组相联组织方式,用得到的替换算法都使用LRU,不过不考虑写回策略。然后用一个\(32\)位的寄存器充当\(4\times8bit\)的Cache块。
老实说,刚开始我一点头绪都没有,因为Cache的工作方式并不是线性的,而是不同模块相互作用,然后就想着摸着石头过河。
也是在这一系列实验中,我深刻的理解了三态门,高阻态,通路复用这些概念的联系,并能够熟练使用。
直接相联
每个地址对应一个cache块,不考虑什么调度算法,缺失的话直接替换覆盖就好。
总共\(16\)位的地址,最低\(2\)位为块内地址,\(8\)个cache块就再拿\(3\)位作为块号,剩下的\(11\)位为标记位,考虑到这里,就可以先画出分线器:
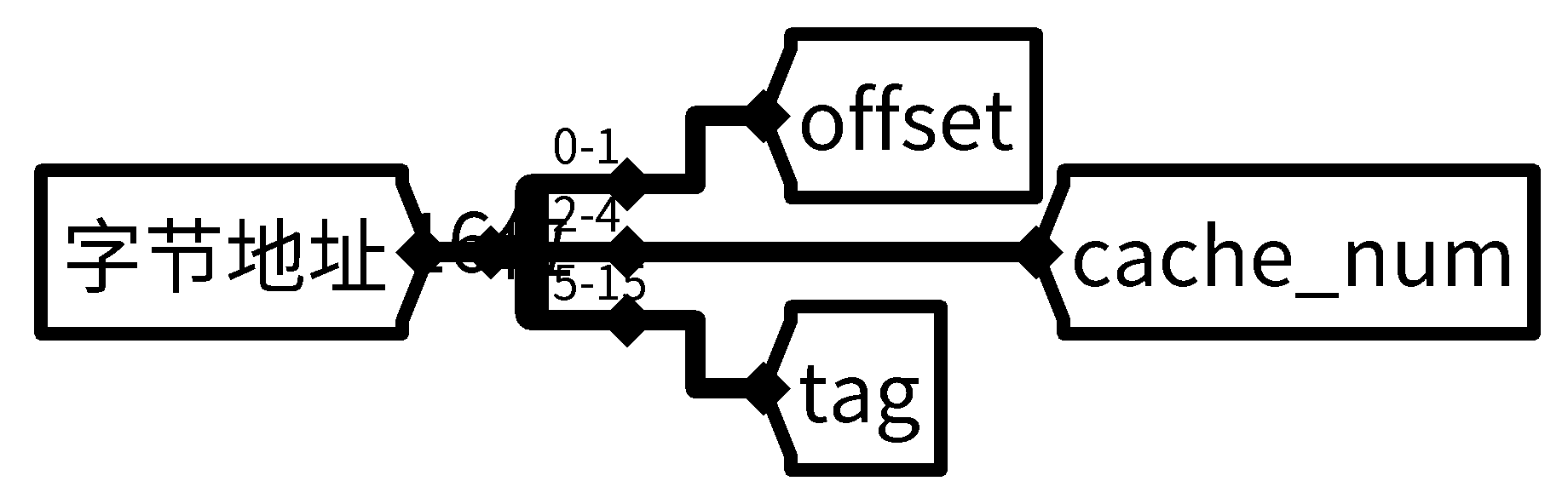
有了块号,就可以确定是哪个cache块被命中了:
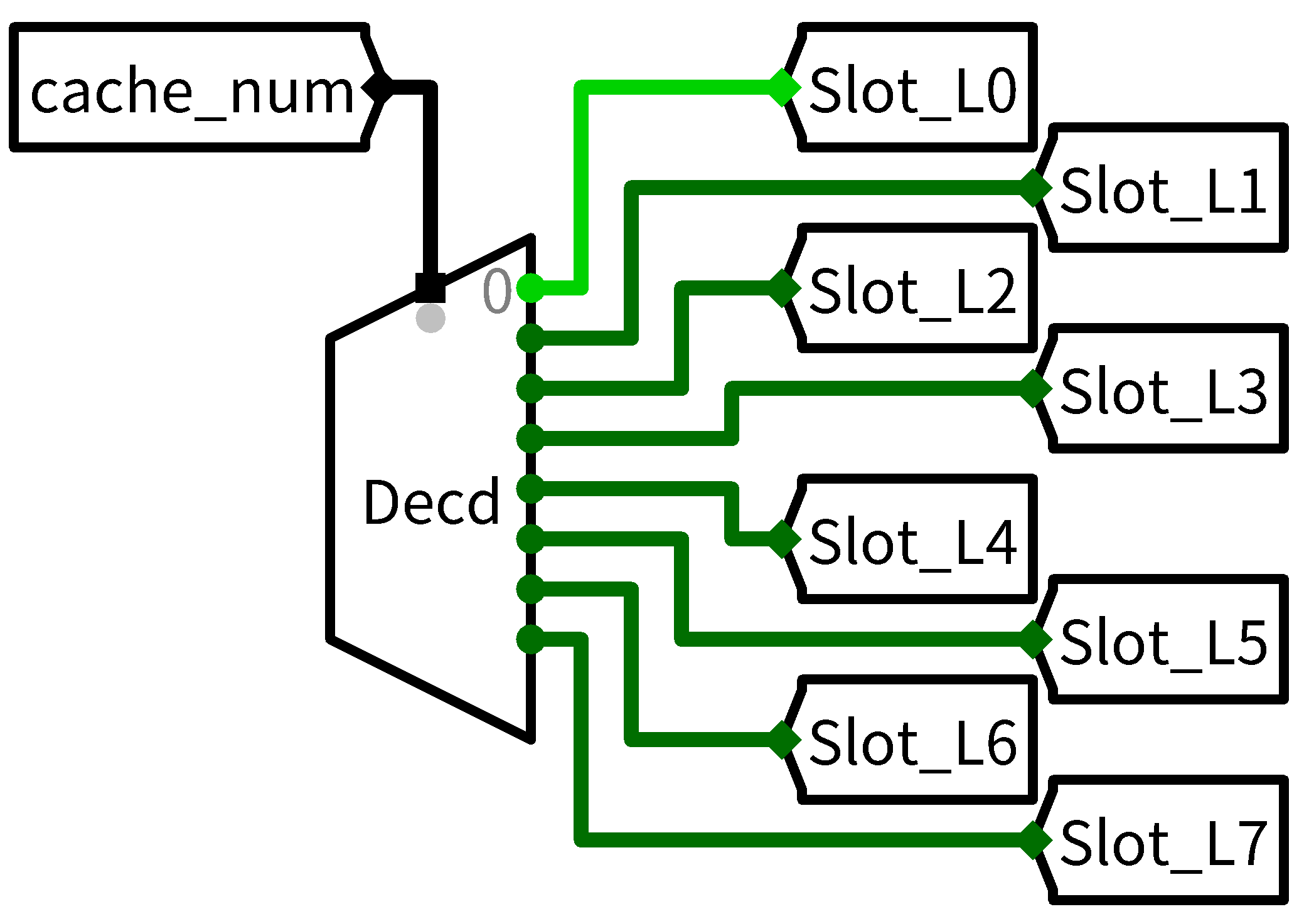
知道了标记位的位数,考虑上有效位,就可以得到一个cache块的构造了:
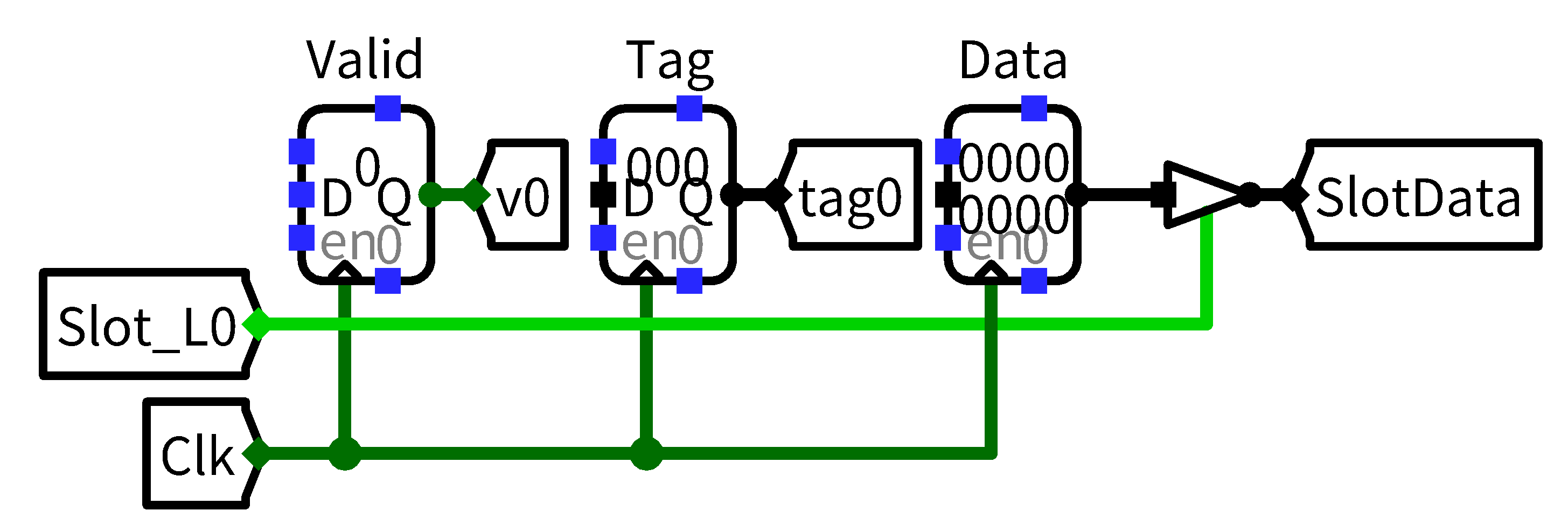
但是只命中cache块不代表访问数据是正确的,需要再考虑有效位以及检查标记位是否相同,综合考量后,得到了缺失判别电路:
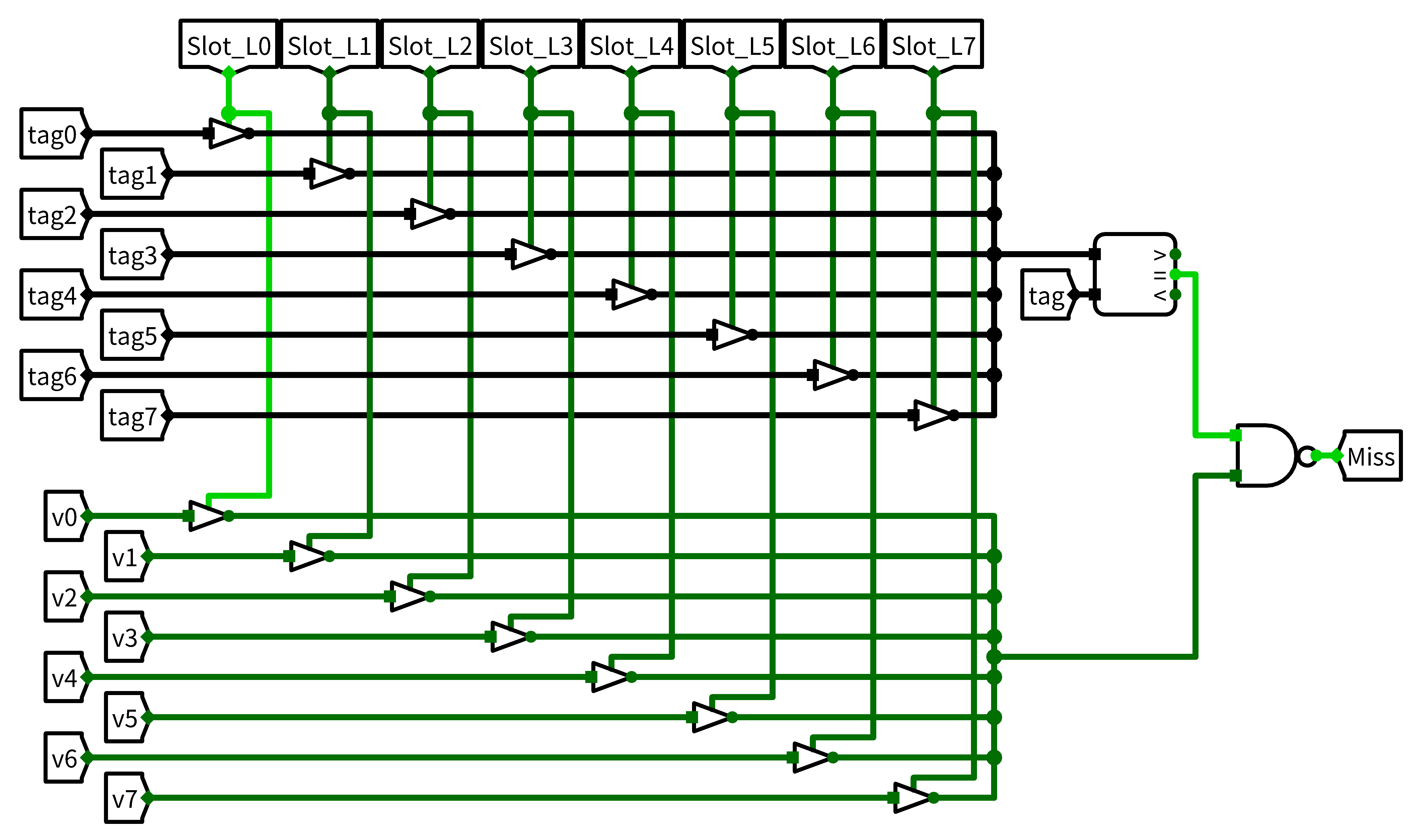
那么,如果是缺失,就需要等待数据被送进来,当BlkDataReady为真后,从BlockDataIn取得数据,并更新命中的cache块,那么,更新相关的逻辑:
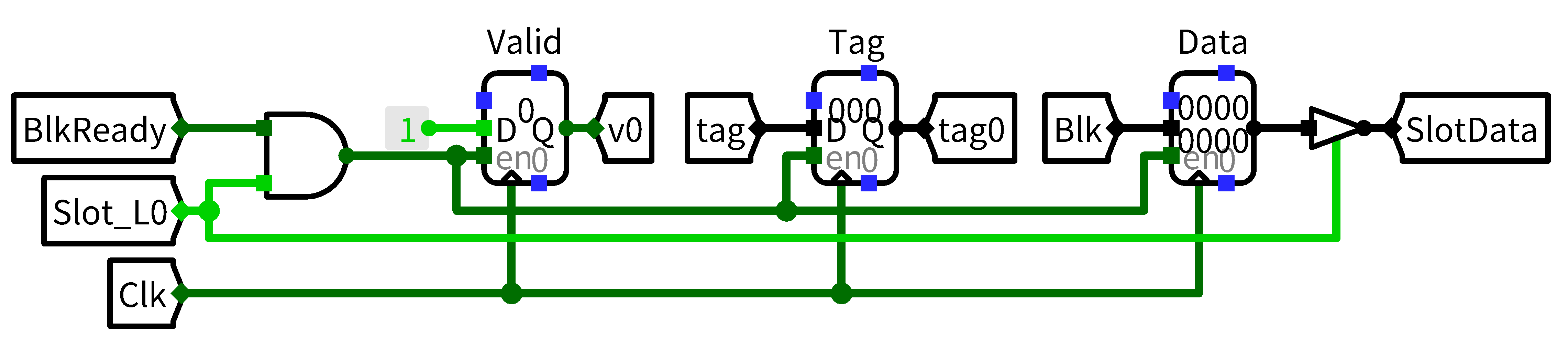
最后,从正确的数据那里把需要的一个字节抠出来:
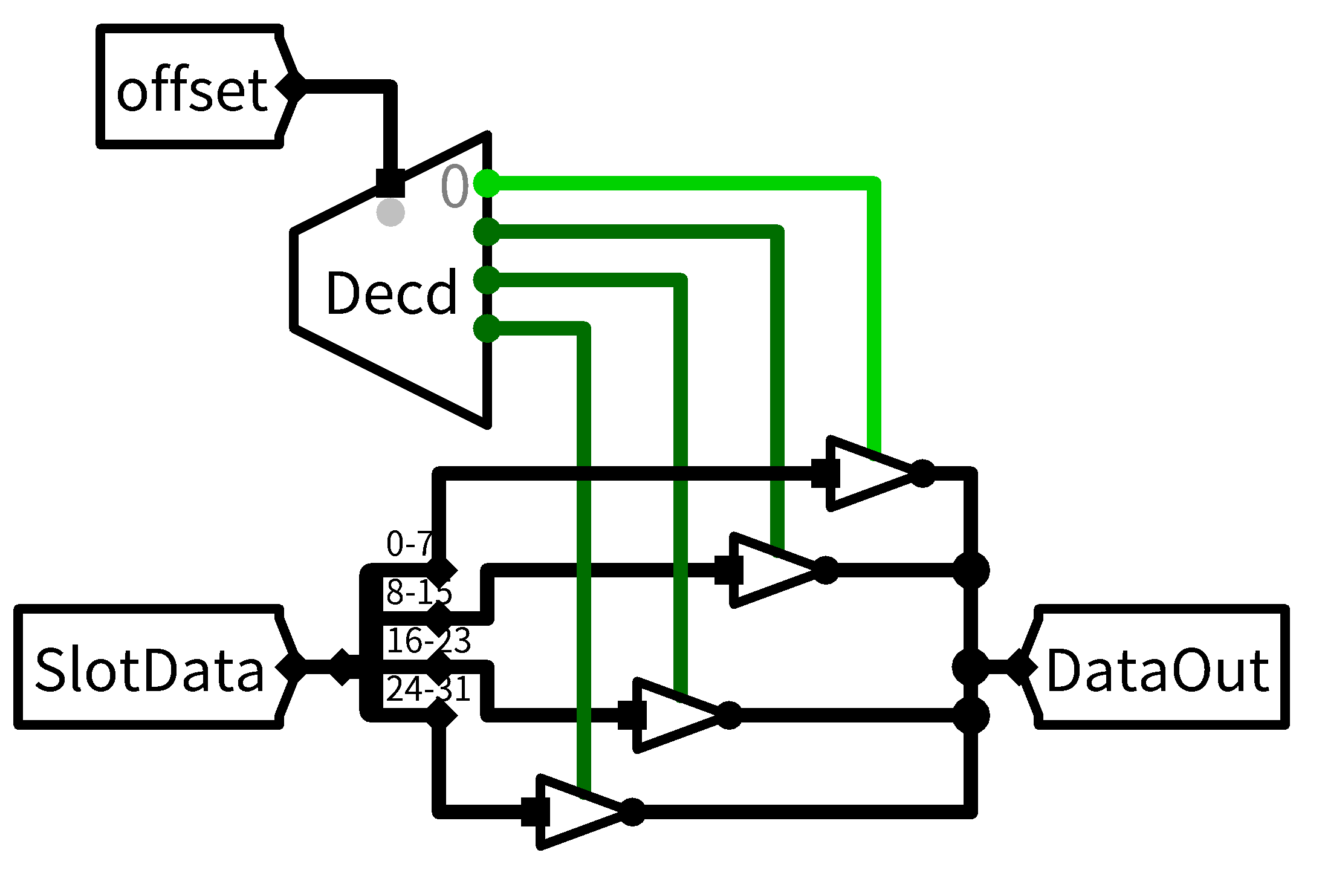
把所有的模块合在一起(我知道画得太乱了TAT):
全相联
全相联的话是所有的地址可以分配到所有的cache块中,这里也是真正开始使用替换算法。
有了直接相联的经验,全相联也更加顺手。
最低\(2\)位依旧为块内地址,剩下的就全是标记位了,于是得到首先的分线器:
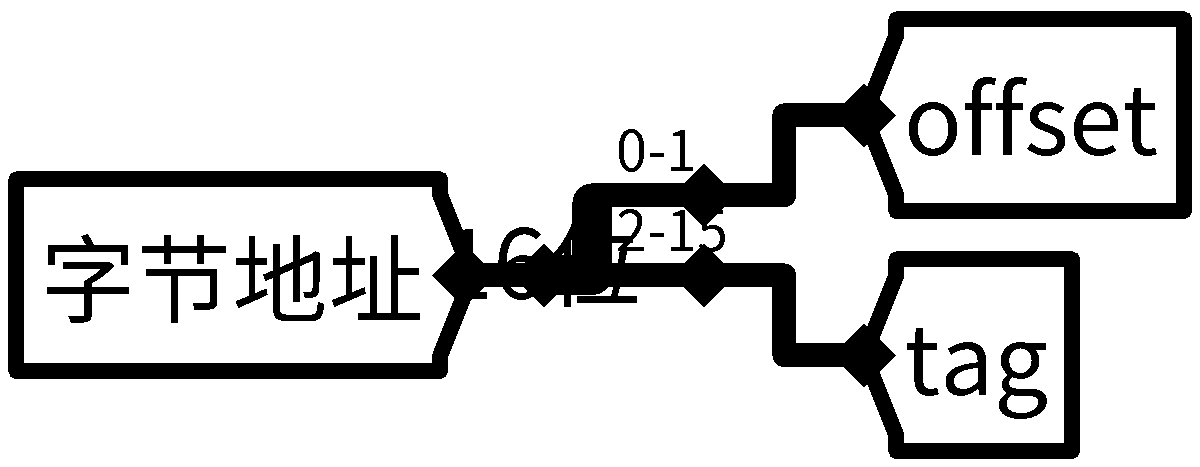
cache块是整个电路图的核心模块,有了标记位的大小后,考虑有效位,用于LRU替换的计数器,再加上数据位,就有了基本的框架。
在直接相联映射中,最终命中的cache块和可能需要替换的cache块是在给出地址后同时确定的,而在全相联映射中,需要经过替换策略得到需要替换的块,然后再进行所有的比较之后才能确定命中的块,就得分开进行。
这里我在回顾的时候陷入了一个误区,全相联映射中需要替换的块难道不一定是最终命中的块吗?这点确实是,但是这是在需要替换的情形下才成立的;如果不需要替换,根据替换策略仍能确定一个需要替换的块,但这个块就不一定是命中块了。
这样确定出一个cache块的内容:
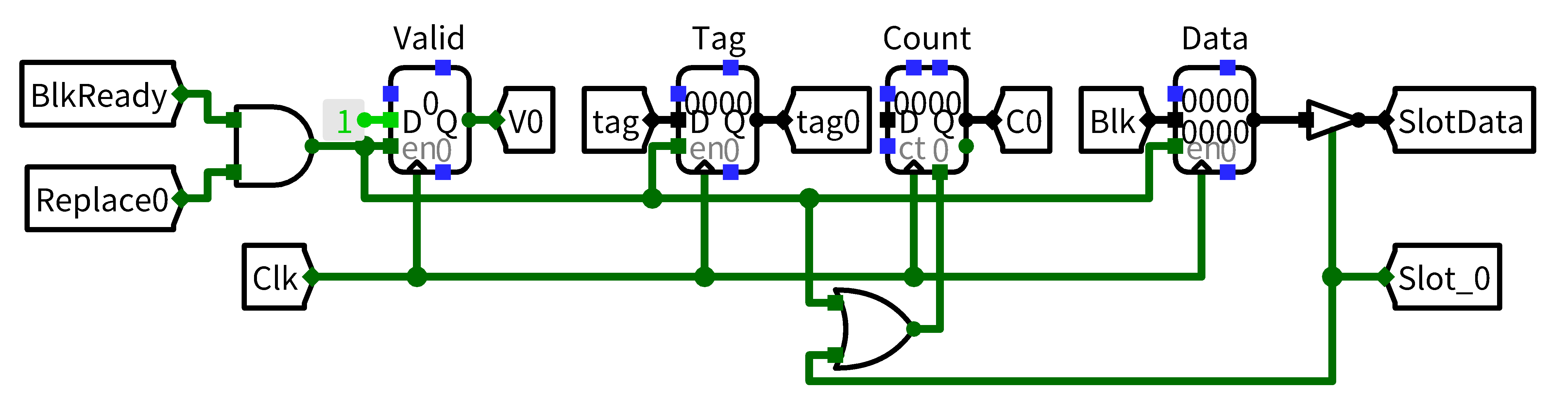
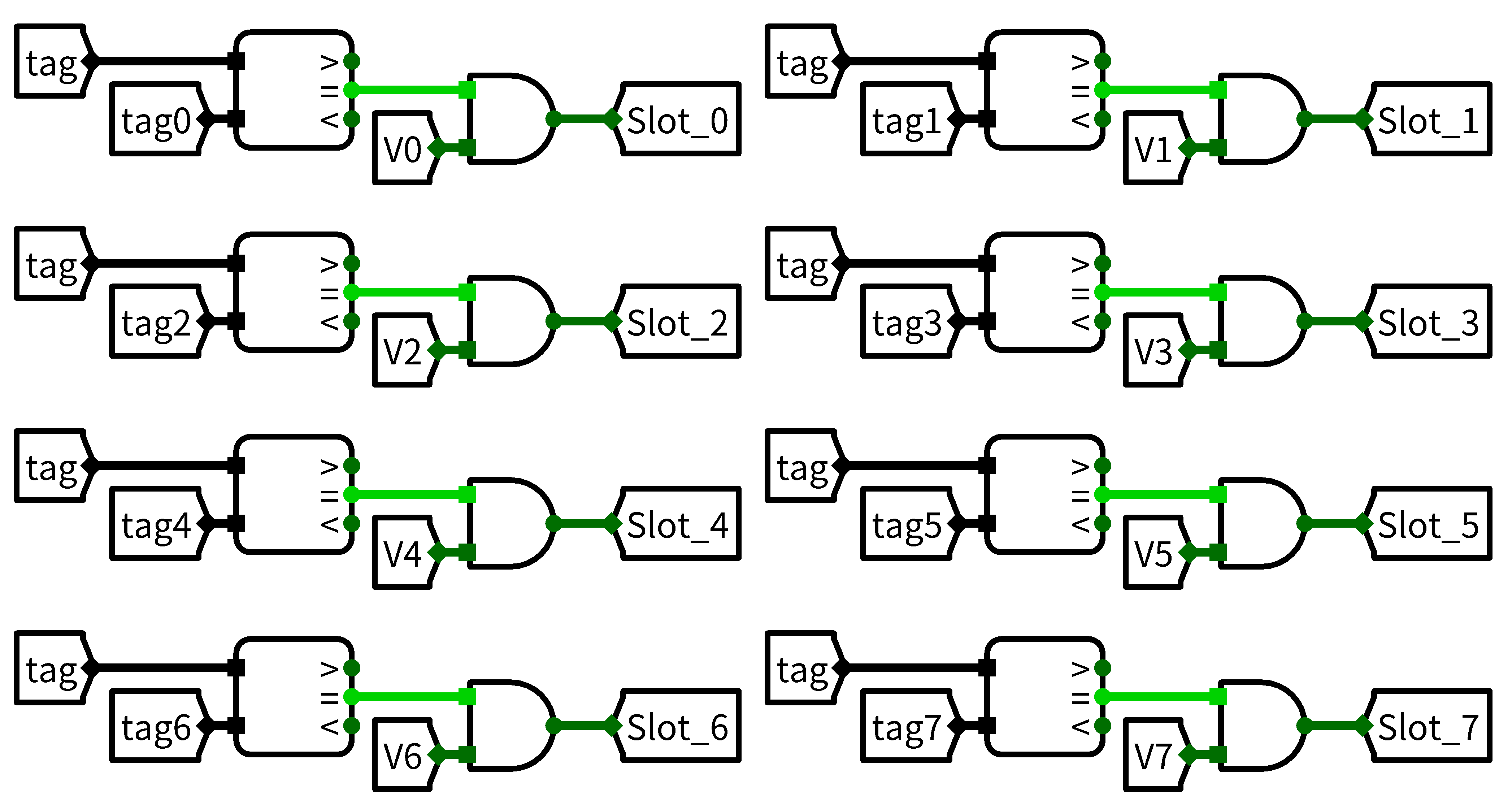
确定命中块和寻找可能需要替换的块可以并行进行,命中很好说,全部比一下就知道是否命中:
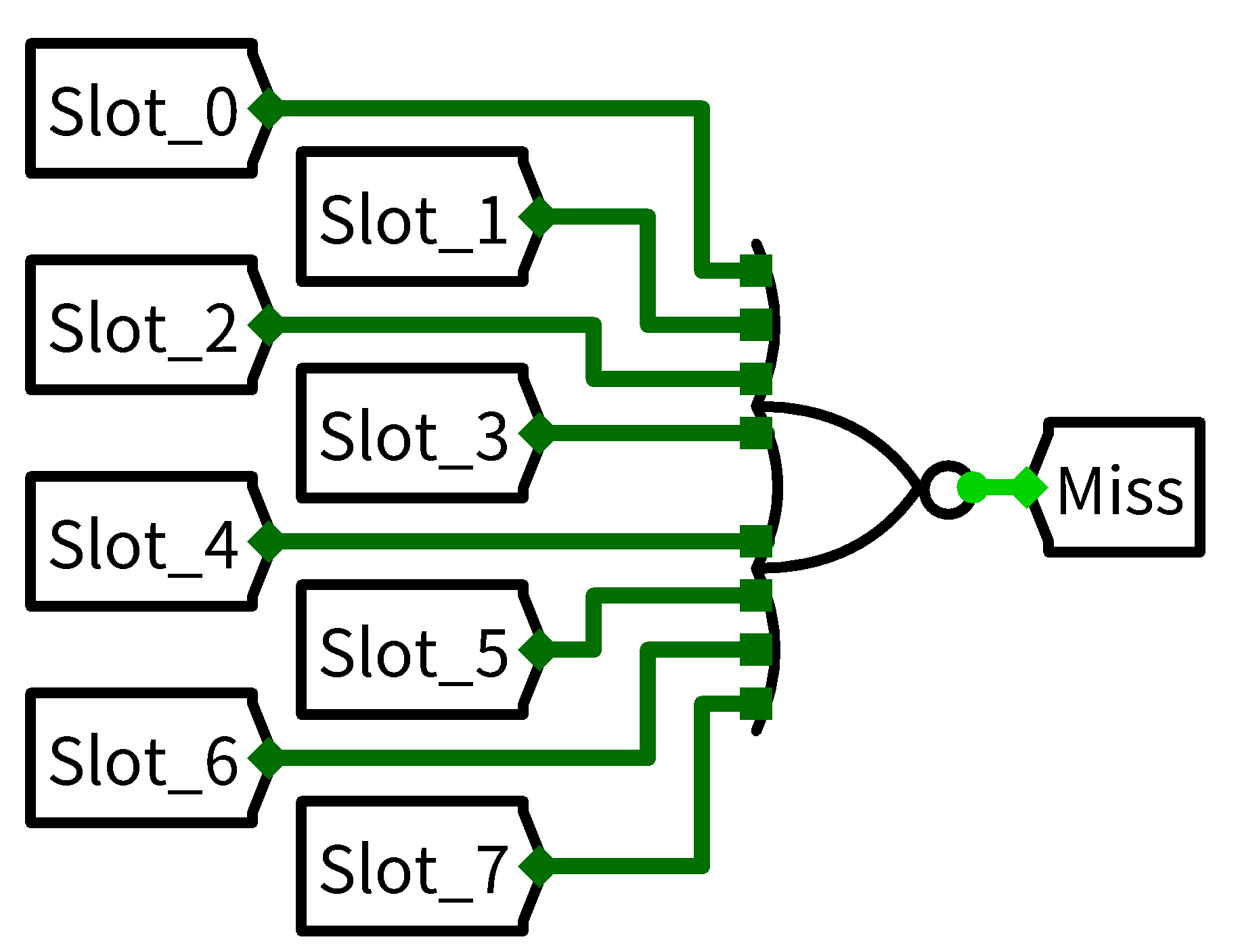
要是都没命中的话自然是miss了:
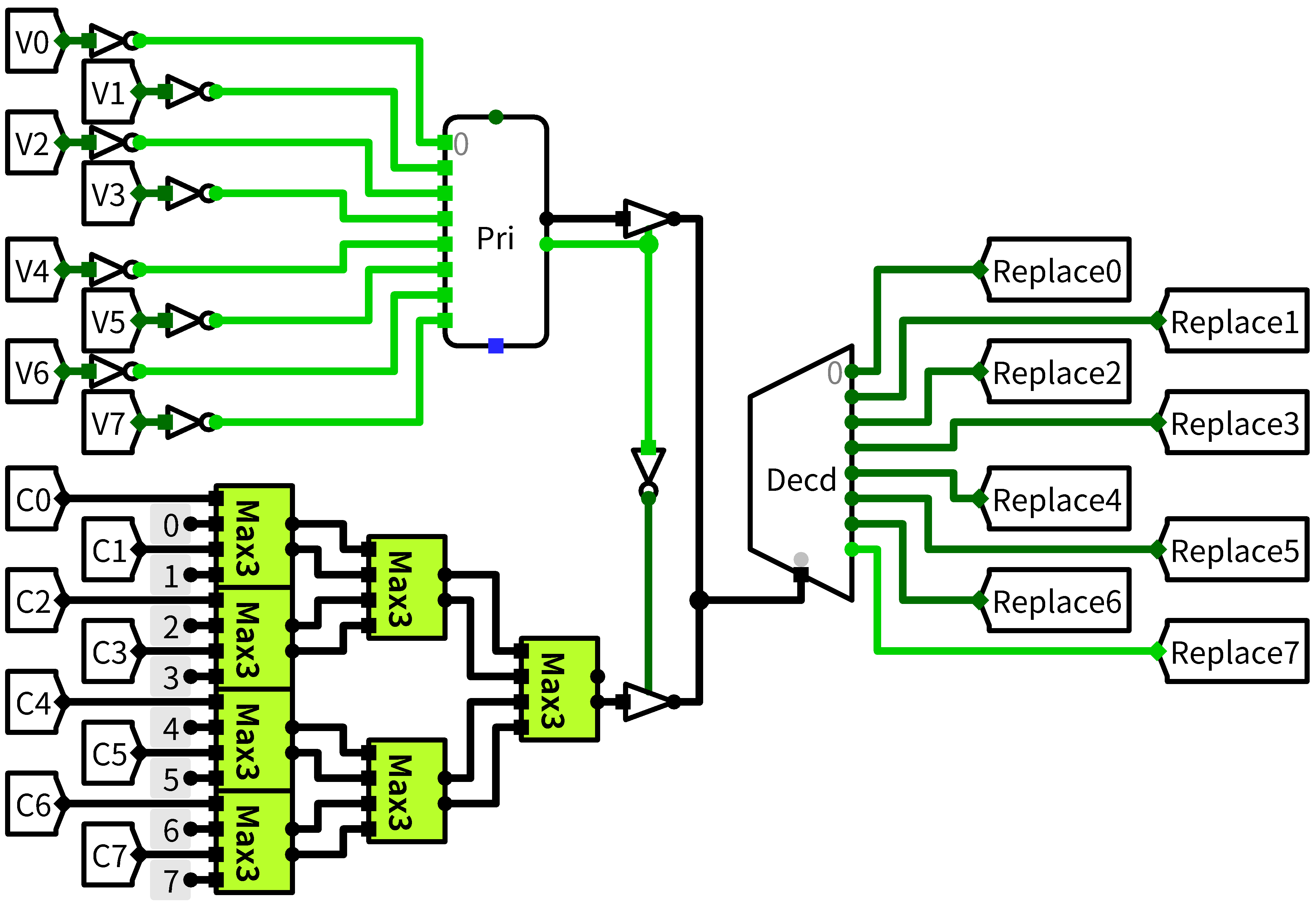
寻找替换块有个优先级,若是存在无效快的话首先选择无效块,否则选择计数器最大的块,两部分也并行进行,最后决定一个:
至于数据完成时的修改替换,已经在之前画cache的时候完成了。
直接复制过来的输出:
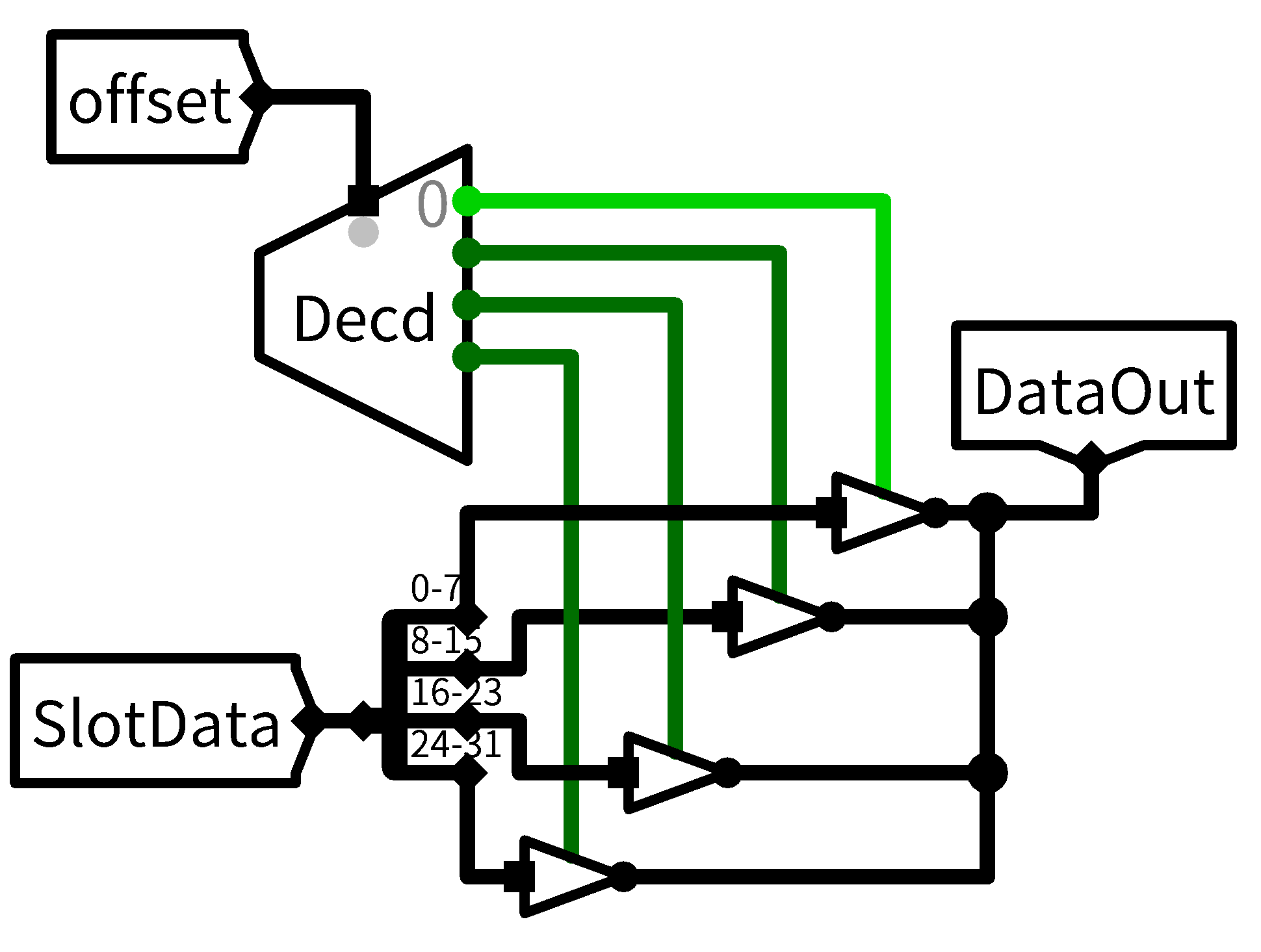
混合在一起!
(我开始理解把图画得清晰一点的重要性了XD
尾声
其实二路组相联其实也做了,但是一直没通过,本来打算也组织一下,但是今天回顾全相联时终于发现哪里错了,就先不整理了,留到下一篇吧。
实验在内存后就是CPU了,然后还有没几天也该开学了,很期待到之后的话我会走到哪里。