Re：从0开始的计算机科学（1）

很惭愧这一周的进度太慢了（明明还是第一周啊啊啊），主要的进展是学了个基础，跟着谭老师的课程做了一些实验，差不多是掌握了基础设计方法，如果类比到C语言的学习的话，就大概是刚学完语法的样子。

我想分成几块块来说说。

logisim

logisim是一个硬件仿真平台，特别像我初次接触C语言时的Dev-C++，偶尔会有奇奇怪怪的bug，然后UI也是一般般，最大的优势是简单友好，安装简单，适用于初学者。

我是在Ubuntu 20.04上进行开发的，这边就稍微整理了一下。通过apt安装的logisim不支持中文，用熟悉了还好，刚用确实是不习惯，我就下载了谭老师课程团队提供的汉化logisim使用，是个jar包。

为了方便使用，我就写了行shell，然后命名为logisim放在了全局里。

1	java -jar /home/frankchen/Applicitions/logisim-hust-linux.jar &

不得不提一句谭老师整个团队是真的厉害，在软件中能看到整个的汉化工作还就是人家做的。

运动码表

因为在大二的暑假曾听过谭老师的课，那时候就推倒了运动码表这块，之后的课听不懂了。所以就有了一定的经验，再从头开始就轻车熟路了许多。

运动码表的功能由一个状态图和各个状态对应的信号组成。

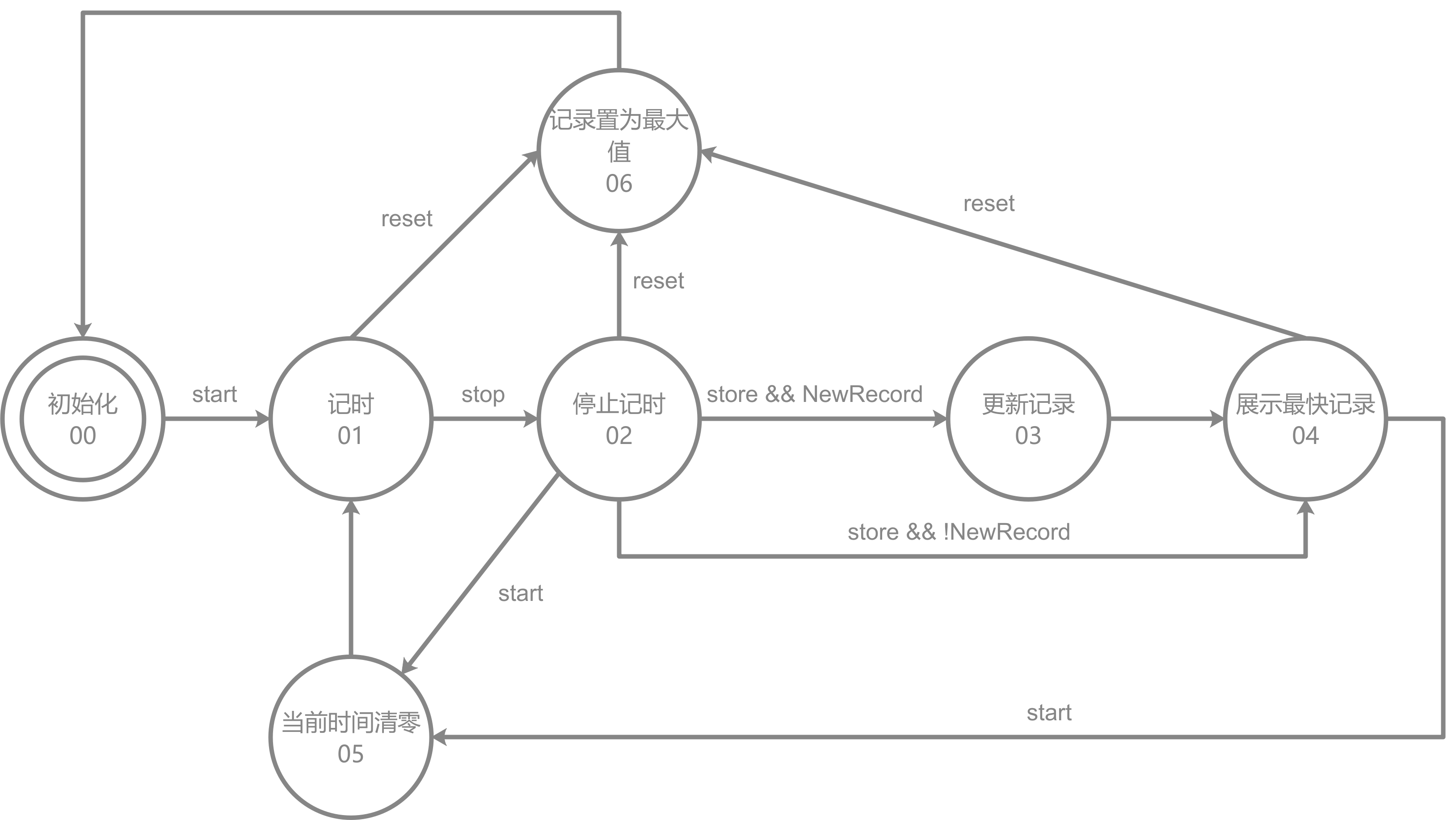
	寄存器来源(9999/计时间器)	寄存器使能	展示来源(寄存器/计数器)	计数器使能	计数器重置
	SDSel	SDEN	DPSEL	TMEN	TMReset
00			1
01			1	1
02			1
03	1	1
04			0
05					1
06	0	1			1

然后填写一下谭老师提供的excel工具，将得到的输入输出关系表达式放到logisim里，就基本上差不多了。

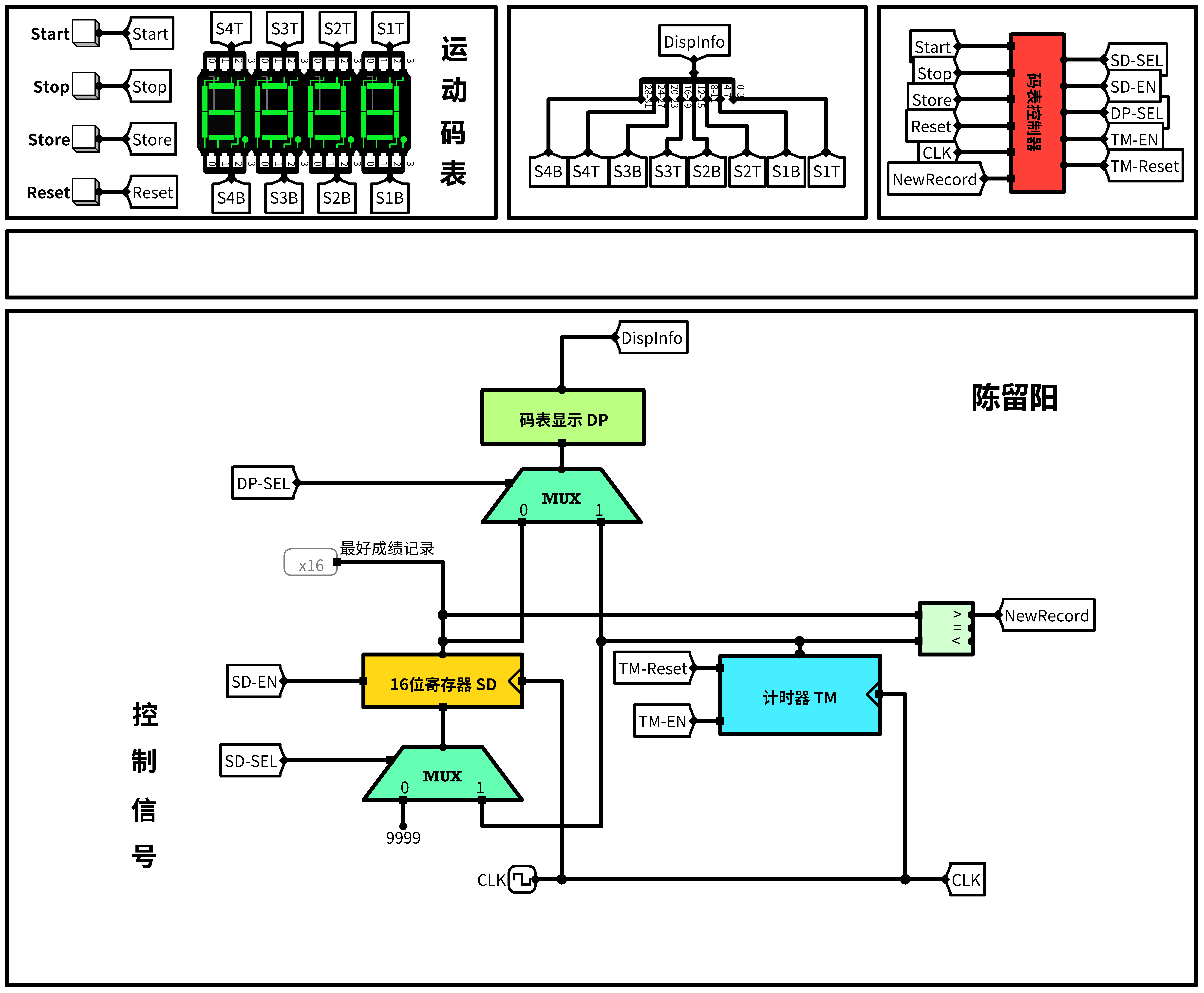
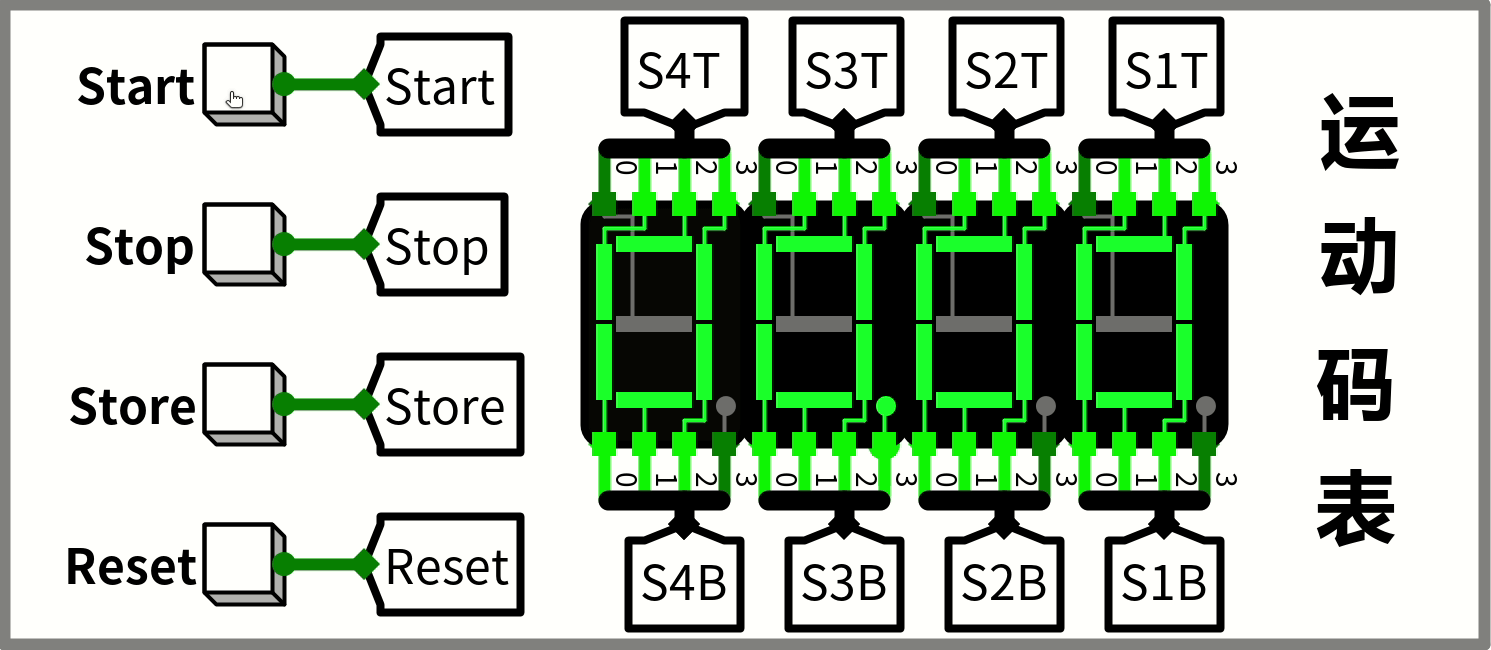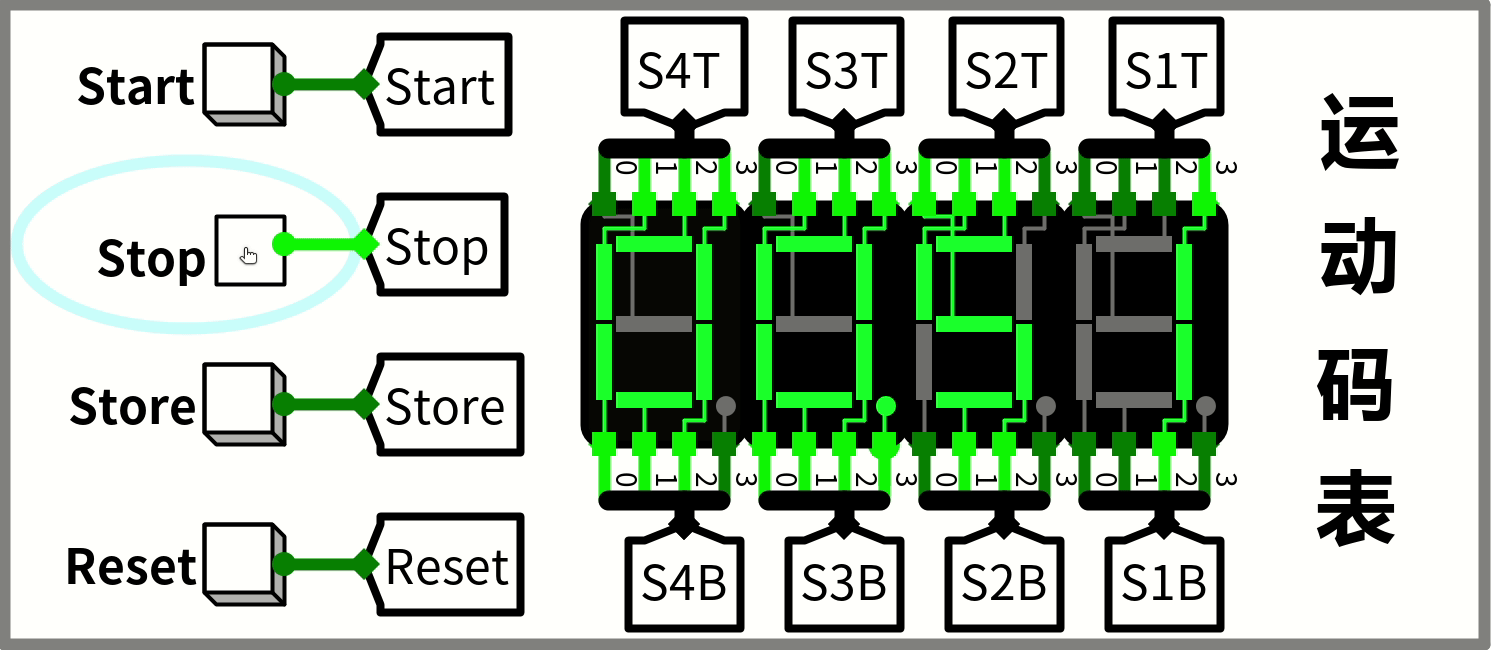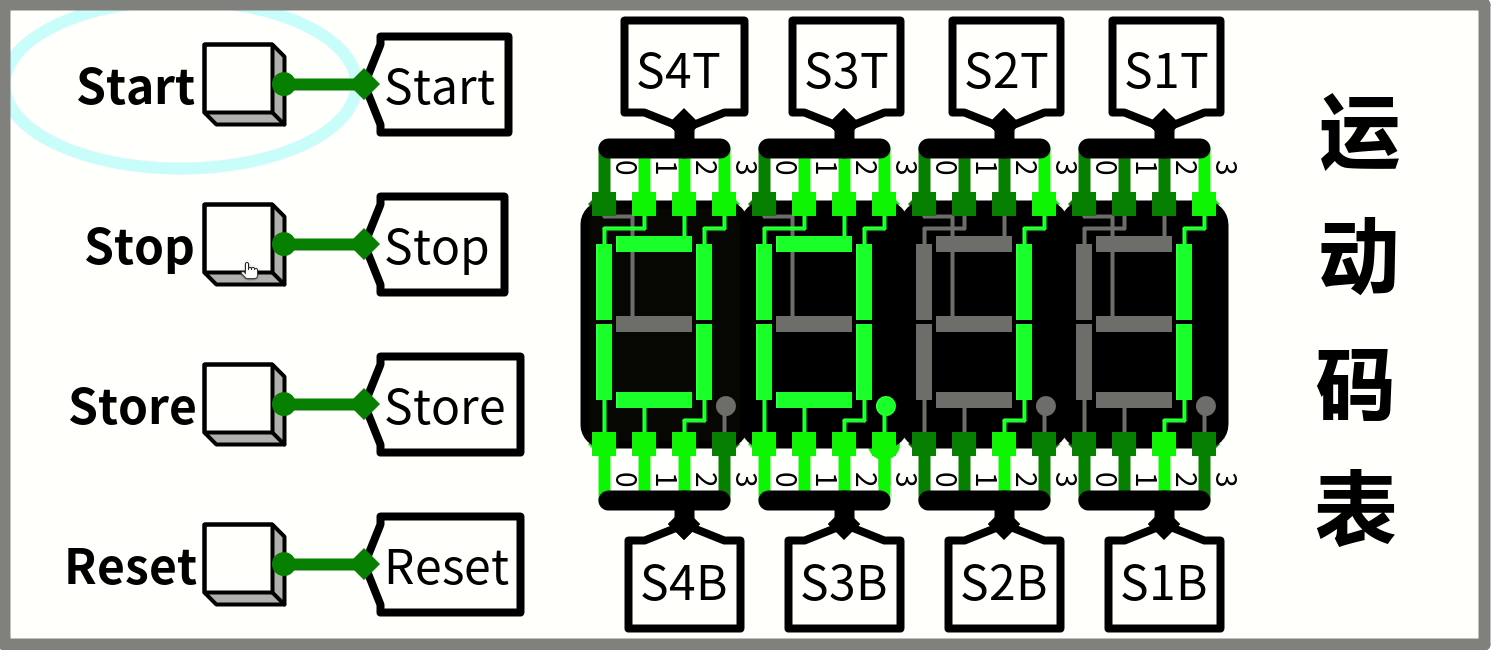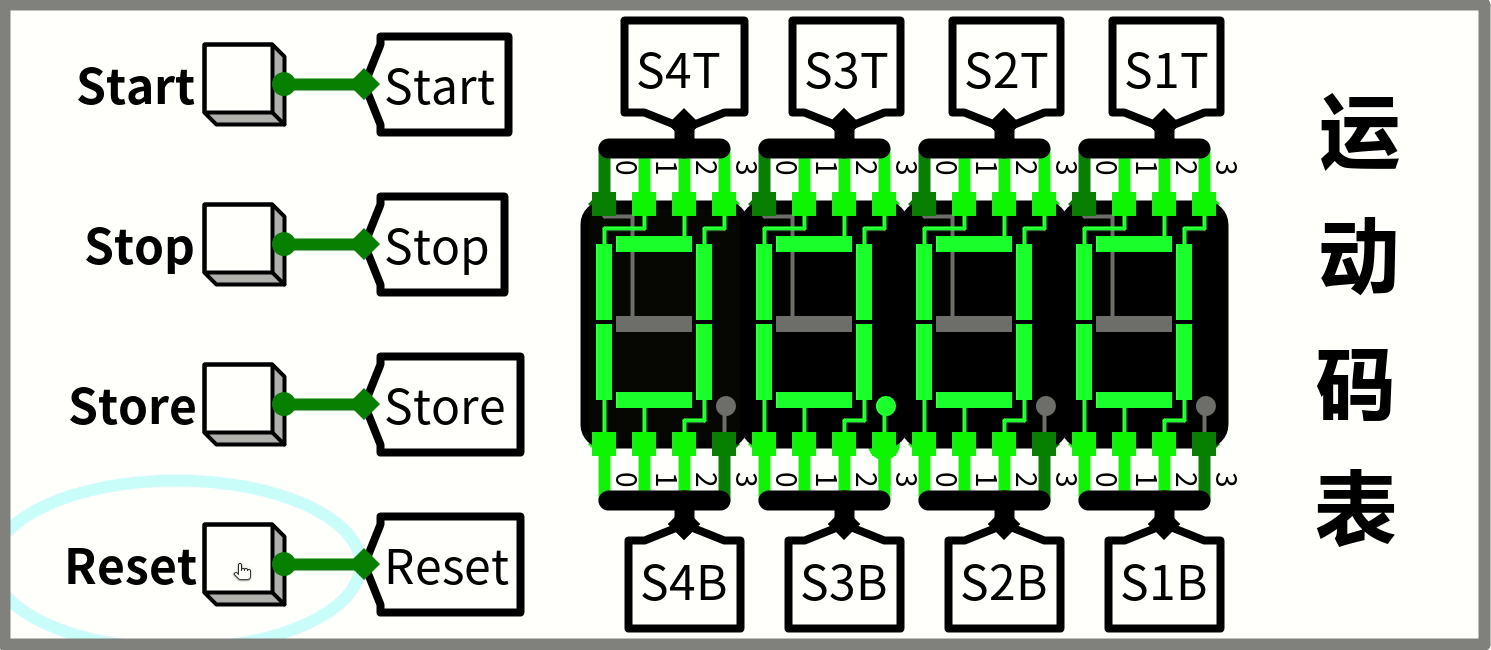
顺便说一句，上边这个gif是用 Peek 录制的，然后状态图的话拿亿图图示画的（我终于决定入正了TAT）。

海明校验码

海明校验码本质上是多重的奇偶校验码，每一位校验码校验几个数，然后每个数被唯一的校验码组合所校验，最后就可以根据出错的校验码组合唯一确定出错的那一位（只出错一位的情况下）顺便纠个错，很巧的是，这种对应关系可以通过二进制来表示。

放上一张从wiki上扒来的图

然后再在最后加一位就能确定是不是一位错，然后就决定是纠错还是报告出错。

判断是不是一位错竟然还是从知乎上看到的。

检测的时候会计算出海明码的校验码E+奇偶校验码P，有以下四种情况：

E=0，P=0 没有错

E≠0，P=1 有一位错，并可以纠正

E≠0，P=0 有两位错，但不能纠正

E=0， P=1 奇偶校验位出错

然后放上我的编码电路与解码电路：

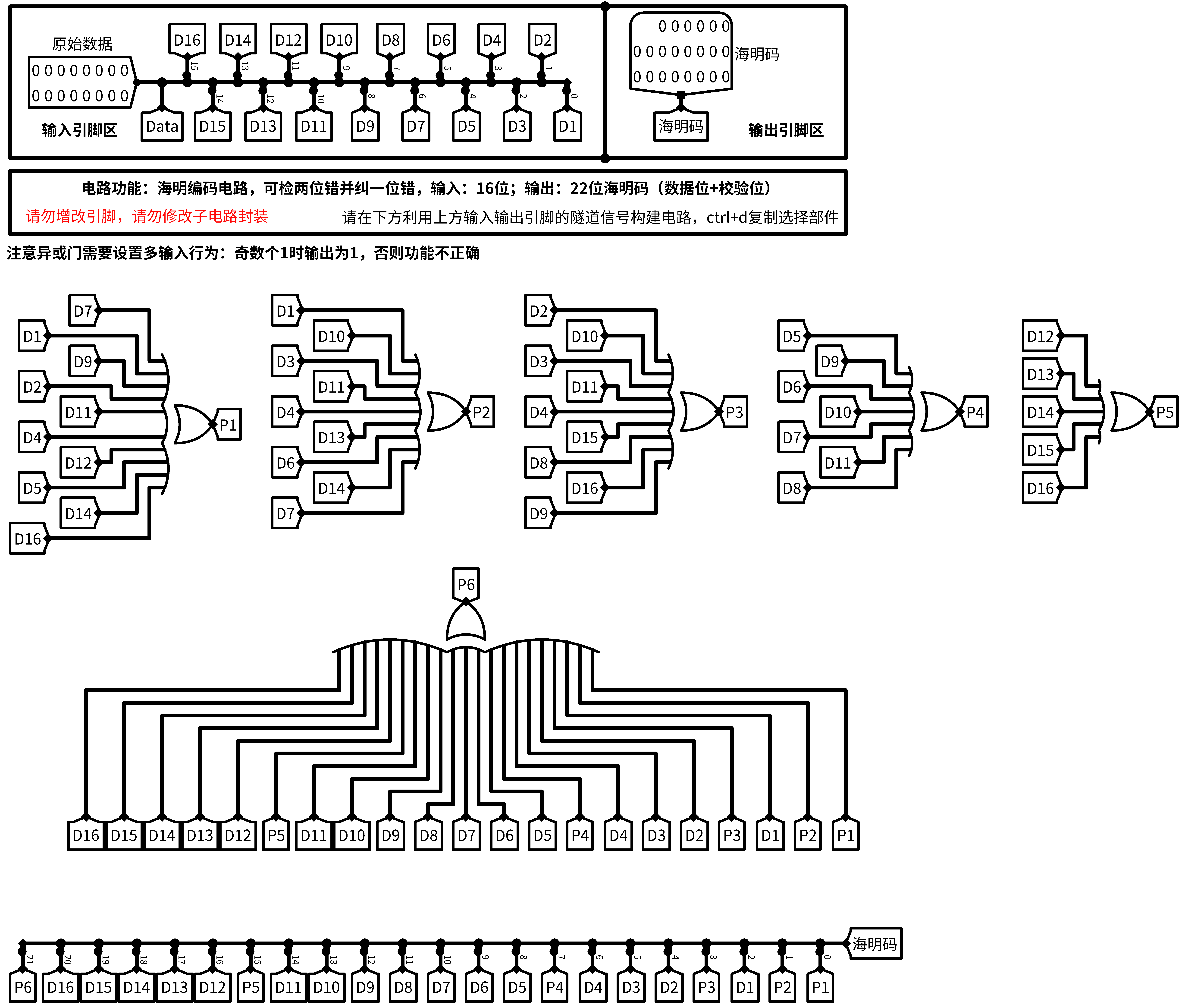
画解码电路的时候我还出了点问题，不知道对第\(i\)位取反应该怎么做，还差点画\(22\)个二路选择器和一个巨型解码器，最终在同学的提示下想到了用位移与异或来解决，思路一下子就开阔了。

2021年2月7日补充

emm，发现这样的海明校验码还是存在问题的，后续发现并修改了：

Re：从0开始的计算机科学（2）

CRC冗余校验码

其实比起海明码，我对CRC更加欢迎，因为在做题过程中，解CRC不需要记很多东西，只用除就好了，除完余数放到最后，再除完看看是不是\(0\)，就很快乐。

然后我就面临一个更加困难的事情，模二除法怎么画？

其实随便一搜就能找到一堆相似的串行画法，通过多个时钟周期，模拟模二除法最终得到结果。

但是要求的是另一种并行的画法，纯组合逻辑解决。

思路就是模二除对异或运算具有分配律，即模二除后异或与异或后模二除答案是相同的，那么，只要预先算好固定长度的CRC编码对一个特定的多项式各个位分别为1的情形下模二除的结果，再根据需要选取几个进行异或，就可以得到结果。

感受到了常数的暴力。

当然，考研都结束了，也不想费力手算了，写了个C++的函数，模拟模二除。

#include <vector>

using namespace std;

/*
 * a.size()=b.size()
 */
vector<bool> XOR(vector<bool> a, vector<bool> b)
{
    vector<bool> c;
    for (size_t i = 0; i < a.size(); i++)
    {
        c.push_back(a[i] ^ b[i]);
    }
    return c;
}

/* 
 * a/b=c...d
 * b is like 1...1
 */
vector<bool> BinaryModuloTwoDivision(vector<bool> a, vector<bool> b)
{
    vector<bool> c, d = {a.begin(), a.begin() + b.size()};
    for (size_t i = 0; i <= a.size() - b.size(); i++)
    {
        if (d.front())
        {
            c.push_back(true);
            d = XOR(d, b);
        }
        else
        {
            c.push_back(false);
        }
        d.erase(d.begin());
        if (i < a.size() - b.size())
            d.push_back(a[i + b.size()]);
    }
    return d;
}

emm，考虑到随机访问并不是硬性需求，其实有很大的优化空间，不过也不是写比赛，就随意了一点。

CRC的纠错比我想象的更为简单，对于CRC，任意一位出错的情况下，进行模二除得到的余数是固定的，反过来说，只要这个余数不是\(0\)，就可以根据对应关系确定出错的位数并加以纠正，如果没有这个对应关系就认为无法纠错。为了实现这个纠错，多项式其实也不是随便选选。

好家伙，研究出CRC的人可真的是厉害。

能查得到的资料都说可以将CRC循环移位到最后一位错然后再纠正，就是个时序电路了，这点我问了问谭老师，老师是这么回答的：

不同的数对应不同的出错位，用一个真值表就可以设计出对应的数字逻辑电路了。

大部分教科书上都介绍循环除法来找到出错位，显然那是不合理的

茅塞顿开。

然后就是CRC的编解码电路：

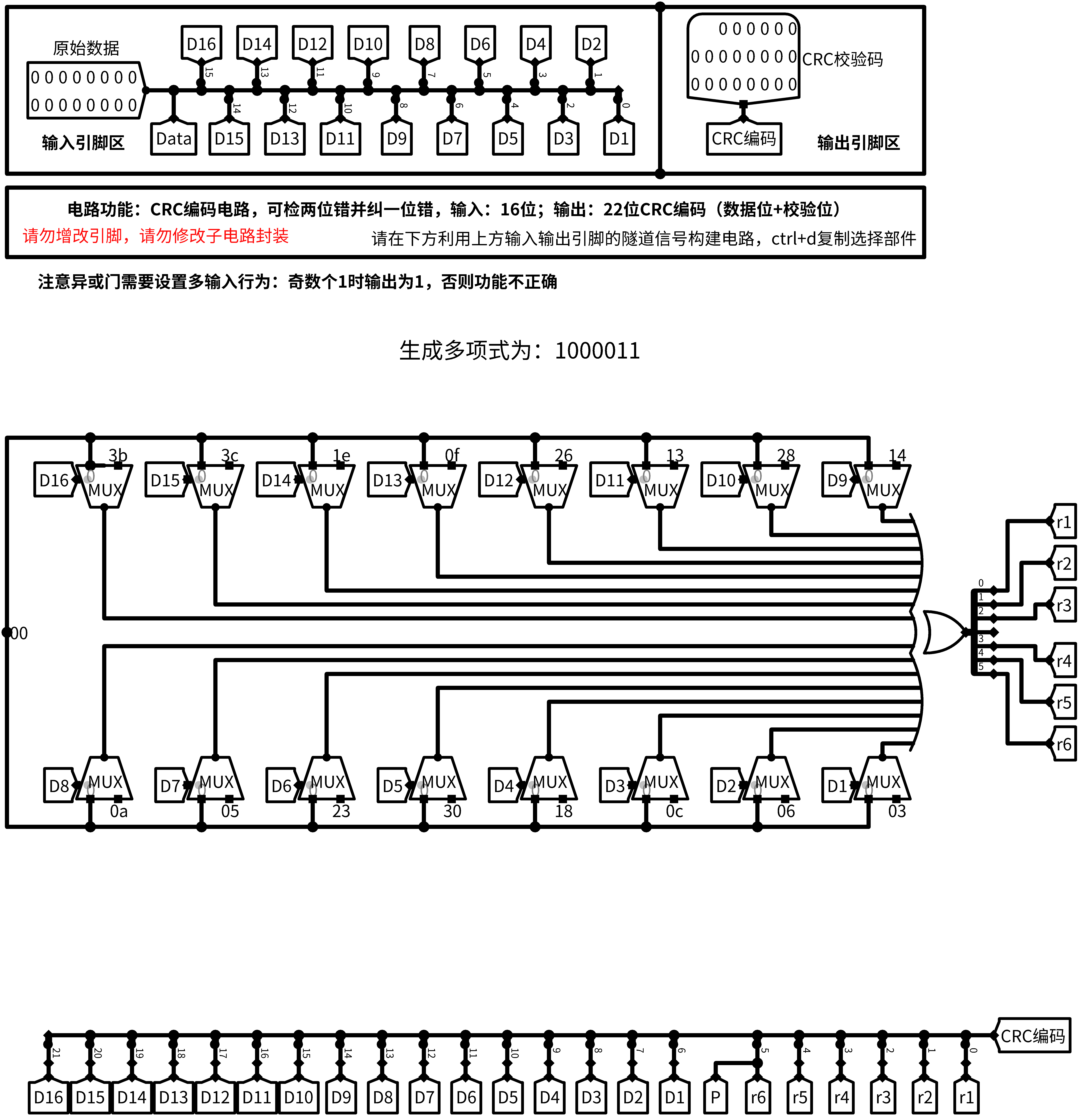
提一嘴，受到故有印象影响，在使用移位然后异或进行纠错的技巧中，我习惯性的用\(1\)进行移位，就会造成实际上需要移的位数减一，画出来的电路就不优雅。

但是事实上可以使用循环移位的方式，把这个\(1\)放到最左边。

刚想到的时候我甚至想跳起来。

2021年2月7日补充

emm，发现这样的CRC冗余校验码还是存在问题的，后续发现并修改了：

Re：从0开始的计算机科学（2）

模拟传输

实际上最开始还画了个国标码转换的电路，加上一个完整的GB2312字库点阵集，就能在logisim中展示中文。

再加上一套老师给定的框架，就能模拟信息传输了，放一个CRC的。

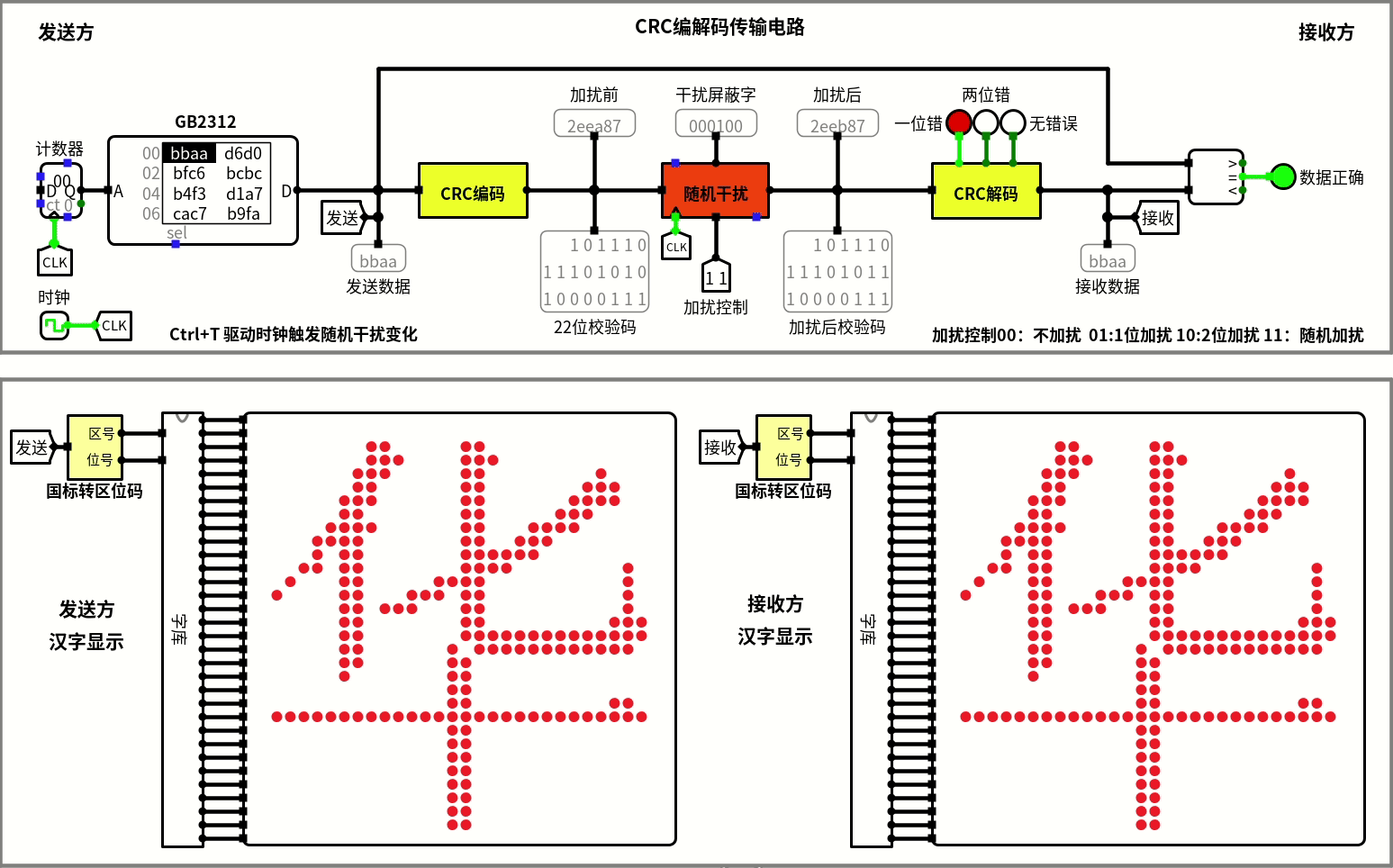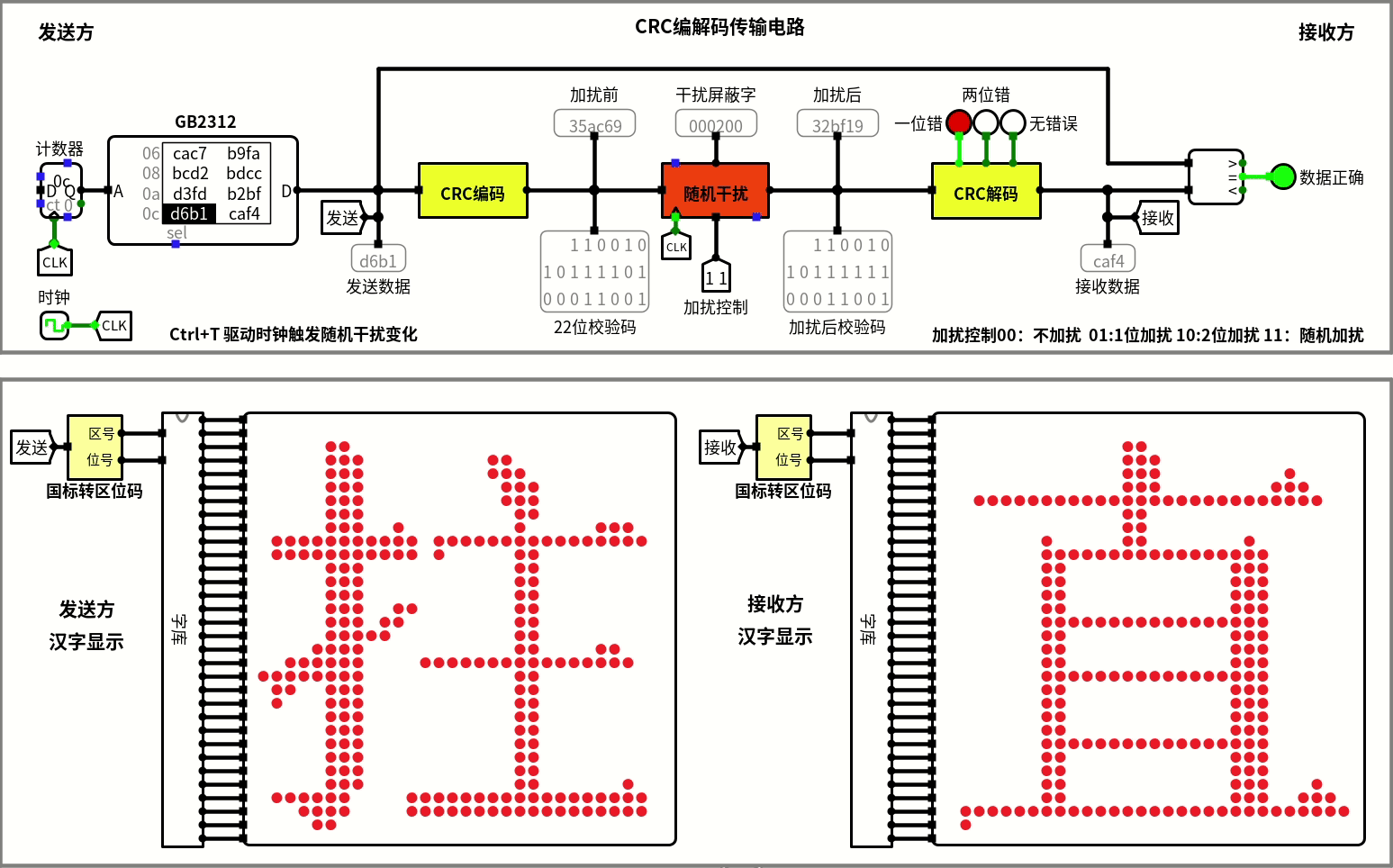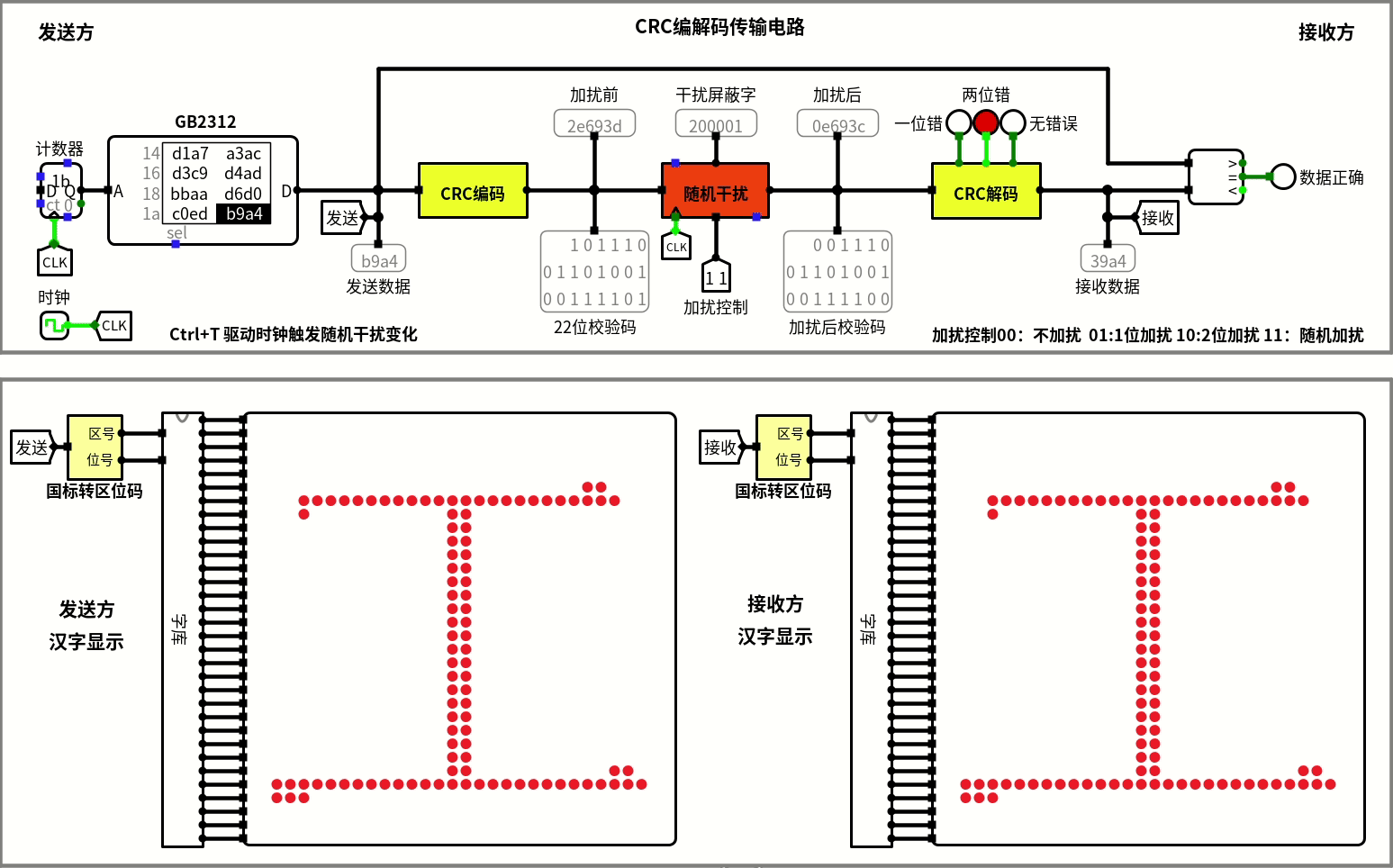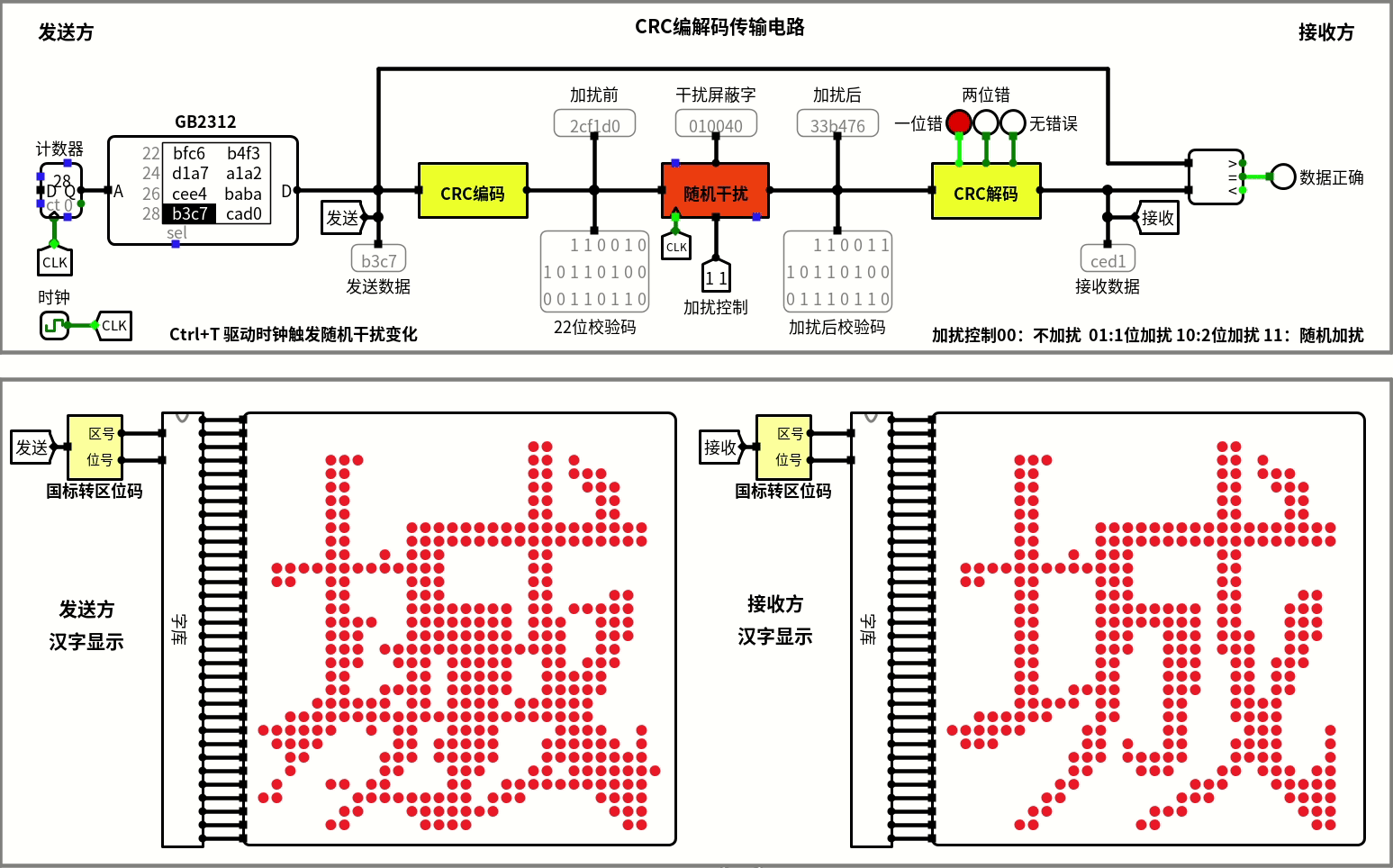
当然，内容也是能改的，我还专门写了个程序，不过也不想麻烦了，做个宣传也是好的。

尾声

老实说这个进展速度我是不太满意的，总是刷视频浪费了我很多的精力，本来三四天的工作量硬生生拖了七天，周日的记录也因为一系列的事情推迟了一天才完成。

嘛，抓紧吧。